GENESIS: Documentation

Equations

The channel conductance was determined by the product of voltage-dependent activation (m) and inactivation (h) gates, and for the Ca²⁺-activated channels a Ca²⁺-dependent activation gate (z)

2+ p 2+ r G(V, [Ca ],t) = ˉgm(V, t) z([Ca ],t) , (units: mV, μM, ms)

(1)

Equations describing the voltage-dependent gates were described from the classic Hodgkin-Huxley [2] scheme

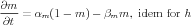∂m ----= αm(1 - m) - βmm, idem for h ∂t

(2)

A E αm(V, t) = ---------------, βm(V, t) = ---------------, idem for αh and βh B + expV+C)∕D F + exp(V +G)∕H

(3)

Activation rates for Ca²⁺-dependent gates were determined by a dissociation constant A and a time constant B

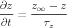∂z-= z∞---z- ∂t τz

(4)

-----1----- z∞ = 1 + ---A---τz = B [Ca2+]

(5)

For the Ca²⁺ channels the Nernst potential [1] was computed continuously. Rectification of Ca²⁺ channels was not modeled using the Goldman-Hodgkin-Katz (GHK) equation [1] because dendritic membrane potentials in this study stayed within a range where Ca²⁺ channels can be considered ohmic (i.e., below -20 mV; Fig. 4.15 in [1] ). Using the simulation results from the final model, we estimate that using the GHK equation with an appropriately scaled maximum conductance ( ) to compensate for differences in driving force would cause only small changes in the amplitude of dendritic Ca²⁺ currents (mean difference 0.7 %, maximum 4.5 %).

References

[1] B Hille. Ionic Channels of Excitable Membranes. Sunderland MA: Sinauer, 1991.

[2] A Hodgkin and A Huxley. A quantitative description of membrane current and its application to conduction and excitation in nerve. Journal of Physiology (Lond.), 117:500–544, 1952.