GENESIS: Documentation

Physical Processes and Model Variables

Mathematical models can be used to describe physical processes that underly the functional activity of biological entities by associating the physical processes with parameters (fixed during a simulation) and variables (computed during a simulation).

As an example, a synaptic current is commonly modeled using a second-order differential equation:

′′ ′ G + αG + βG = S

(1)

with S = δ(t - t₁) + ⋅⋅⋅ + δ(t - t_N).

In computational neuroscience the right-hand side of this equation corresponds to the level of synaptic activation delivered by spikes arriving at times t_i.

Assuming the initial values G(0) = 0 and G′(0) = 0, the solution to this equation is a dual-exponential equation:

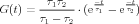τ1τ2 -t -t G(t) = -------⋅ (e τ1 - e τ2 ) τ1 - τ2

(2)

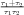with α = τ1+τ2-
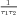τ1τ2 and β = -1--
τ1τ2 . This equation has two parameters TAU1 and TAU2, sometimes called the rise and decay time constants, respectively. Assigning values to the two parameters, this can be expressed in the NDF File Format as:

  PARAMETERS
    PARAMETER ( TAU1 = 0.50e-3 ),
    PARAMETER ( TAU2 = 1.20e-3 )
  END PARAMETERS

When one biological entity modulates the behavior of another, their physical processes share one or more variables. In the case of a synaptic channel the incoming spikes raise the neurotransmitter concentration level in the synaptic cleft, which then modulates total ionic conductance through channels in the post-synaptic membrane. The NDF file format expresses the neurotransmitter concentration level as activation and conductance as G. As these variables are shared they must be declared using the BINDABLES keyword:

  BINDABLES
    INPUT activation, OUTPUT G
  END BINDABLES

Assuming a synapse is present under the label ../synapse, its activation level can be bound to the channel activation level using a BINDINGS clause:

  BINDINGS
    INPUT ../synapse->activation
  END BINDINGS

Putting everything together using the EQUATION_EXPONENTIAL token to represent the dual-exponential equation, we get the NDF snippet that defines a model’s component with name ’exp2’:

EQUATION_EXPONENTIAL exp2
  BINDABLES
    INPUT activation, OUTPUT G
  END BINDABLES
  BINDINGS
    INPUT ../synapse->activation
  END BINDINGS
  PARAMETERS
    PARAMETER ( TAU1 = 0.50e-3 ),
    PARAMETER ( TAU2 = 1.20e-3 )
  END PARAMETERS
END EQUATION_EXPONENTIAL

In this example, the order of the clauses of BINDABLES, BINDINGS and PARAMETERS was chosen for readibility. Note: Neither the NDF file format nor the Model Container makes a syntactical distinction between the variables and parameters of a physical process.

The NDF format supports an extensible set of tokens including SEGMENT, CHANNEL, CELL, POPULATION, PROJECTION, NETWORK and many more that allow the construction of models ranging from subcellular dynamics up to the network level.