



Next: Exponential Euler
Up: Numerical Schemes
Previous: Forward-Euler
Contents
The backward-Euler method also truncates the Taylor series after two
terms. The difference is that the derivative is evaluated at point
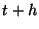 instead of at point
instead of at point 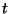 .
.
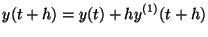 |
(1.3) |
Assuming that the value at point  is correct, the backward-Euler
method computes the value at point
is correct, the backward-Euler
method computes the value at point 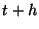 with a local truncation error
that scales with
with a local truncation error
that scales with 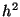 . The backward-Euler method always gives
undershoots on the original curve.
. The backward-Euler method always gives
undershoots on the original curve.
Normally we do not know the derivative at point 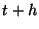 , although we
need it to compute the function value at point
, although we
need it to compute the function value at point 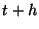 . In practice
this requires a rearrangement of the equation. We call such a
numerical scheme an implicit numerical scheme. For most
equations implicit schemes are more stable than explicit schemes
because of the undershoots.
. In practice
this requires a rearrangement of the equation. We call such a
numerical scheme an implicit numerical scheme. For most
equations implicit schemes are more stable than explicit schemes
because of the undershoots.
Figure:
Graphical illustration of
the backward-Euler method. To obtain point 2 from point 1, we
take the derivative at point 2 and extrapolate it at point 1. To
obtain point 3 starting at point 2, we do the same: take the
derivative at point 3 and extrapolate it at point 2.
![\includegraphics[scale=0.6]{figures/beuler.eps}](img21.png) |




Next: Exponential Euler
Up: Numerical Schemes
Previous: Forward-Euler
Contents
2002-11-15
![]() is correct, the backward-Euler
method computes the value at point
is correct, the backward-Euler
method computes the value at point ![]() with a local truncation error
that scales with
with a local truncation error
that scales with ![]() . The backward-Euler method always gives
undershoots on the original curve.
. The backward-Euler method always gives
undershoots on the original curve.
![]() , although we
need it to compute the function value at point
, although we
need it to compute the function value at point ![]() . In practice
this requires a rearrangement of the equation. We call such a
numerical scheme an implicit numerical scheme. For most
equations implicit schemes are more stable than explicit schemes
because of the undershoots.
. In practice
this requires a rearrangement of the equation. We call such a
numerical scheme an implicit numerical scheme. For most
equations implicit schemes are more stable than explicit schemes
because of the undershoots.
![\includegraphics[scale=0.6]{figures/beuler.eps}](img21.png)