



Next: Backward-Euler
Up: Numerical Schemes
Previous: Numerical Schemes
Contents
The forward-Euler method truncates the Taylor series after two
terms:
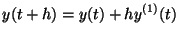 |
(1.2) |
Assuming that the value at point  is correct, the forward-Euler
method computes the value at point
is correct, the forward-Euler
method computes the value at point  with a local error that
scales with
with a local error that
scales with  (see the first term of the error series). The
forward-Euler method always gives overshoots on the original curve.
(see the first term of the error series). The
forward-Euler method always gives overshoots on the original curve.
Figure 1.1:
Graphical illustration of the forward-Euler method for an
exponential like curve. Starting at point 1, the tangent of the
curve is taken and linearly extrapolated to obtain point 2. There
again the same procedure is used to obtain point 3. Note that
point 2 lies on curve 2 and point three lies on curve 3, both of
which are offset against the original curve.
![\includegraphics[scale=0.6]{figures/feuler.eps}](img19.png) |
2002-11-15
![]() is correct, the forward-Euler
method computes the value at point
is correct, the forward-Euler
method computes the value at point ![]() with a local error that
scales with
with a local error that
scales with ![]() (see the first term of the error series). The
forward-Euler method always gives overshoots on the original curve.
(see the first term of the error series). The
forward-Euler method always gives overshoots on the original curve.
![\includegraphics[scale=0.6]{figures/feuler.eps}](img19.png)