



Next: Numerical Schemes
Up: Numerical Preliminaries
Previous: Numerical Preliminaries
Contents
If we denote with
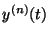 the function value at point
the function value at point  of the
of the
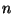 'the derivative of a function
'the derivative of a function  , then the Taylor series of a
continuous
function
, then the Taylor series of a
continuous
function  at point
at point  is given by:
is given by:
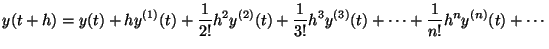 |
(1.1) |
Some remarks about this expansion:
 can be any element of
can be any element of
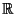 , such that a function is
completely defined by its Taylor expansion at any single point of
its domain. (Full knowledge of the function at a single point
determines the full function at all points).
, such that a function is
completely defined by its Taylor expansion at any single point of
its domain. (Full knowledge of the function at a single point
determines the full function at all points).
- The successive terms of the Taylor series are decreasing in
magnitude in an exponential way.
- We can truncate a Taylor series to approximate the original
function. This divides the Taylor series in two separate series:
the numerical scheme and the error series. The error after
truncation is mainly dependent on the first term of the error
series.




Next: Numerical Schemes
Up: Numerical Preliminaries
Previous: Numerical Preliminaries
Contents
2002-11-15
![]() the function value at point
the function value at point ![]() of the
of the
![]() 'the derivative of a function
'the derivative of a function ![]() , then the Taylor series of a
continuous
function
, then the Taylor series of a
continuous
function ![]() at point
at point ![]() is given by:
is given by: